文 | HW君
当我们在谈论熵时,我们在谈论些什么。
——HW君
系列文章:
1. 尺熵系统与被测熵系统
在上一期《信息哲学 | #2 信息的HW诠释》我们提出了「信息是0熵系统」的观点。
不过这几天HW君重新思考,认为「信息是0熵系统」的说法并不妥当。
首先「信息是熵系统」的说法是没问题的。
但断言「信息的熵为0」则是HW君用了另外一个作为基准的「0熵系统」对信息进行测量后得出的结论。
如果采用不同的基准去测量,那么同一个信息也会得到不同的非0熵。
因此「信息是0熵系统」这样的结论并不严谨。
这就是还没有想明白便开始写文章的坏处,不过也没有办法,边写边迭代才是效率最高的做法。
在思索许久之后,HW君决定用「尺熵系统」和「被测熵系统」来替换原来的概念。
一个信息,它毫无疑问是一个熵系统,信息依赖物质和能量。
这个信息可以作为一个「尺熵系统」,去测量其他不同的「被测熵系统」,得到不同「被测熵系统」的熵值。
它也可以作为一个「被测熵系统」,被其他不同的「尺熵系统」所测量,而得到自身的不同熵值。
这样的表述才是完整的。
2. 指代熵系统
回顾一下到第一期《信息哲学 | #1 信息是熵还是负熵?》。
面对「公式计算出来的香农信息量」和「直观感受到的日常信息量」之间的矛盾感,人们发明了一些补丁。
这些补丁大致可以分为两大类:
补丁1:加入时间概念。
把信息分成已知信息和未知信息,日常生活使用「信息量」时是指已知信息的「信息量」。
补丁2:否认两种概念相同。
即认为同一个事物存在两套数学性质不同的信息,因而能得出两种不同的信息量,它们的使用场景不同。
日常生活中,其实经常出现像「补丁1」这样的「已知信息量」的情况。
我们看这样的一个场景:
HW君有一个4GB的U盘,然后HW君往U盘里复制了一个1GB的文件,于是还剩下3GB的空间。
这个场景描述的是一个我们日常生活中司空见惯的事情。
上面这个复制文件的例子中,描述文件大小的单位是GB,也就是Gigabyte,它可以进行下面这样的换算:
1 GB = 1024 MB = 10242 KB = 10243 B = 10243*8 bit
也就是说,我们经常使用到的硬盘容量、文件大小等概念,其实它们都是熵(信息量/信息熵/香农熵),单位为bit。
这些熵的求解,都符合香农信息量公式。
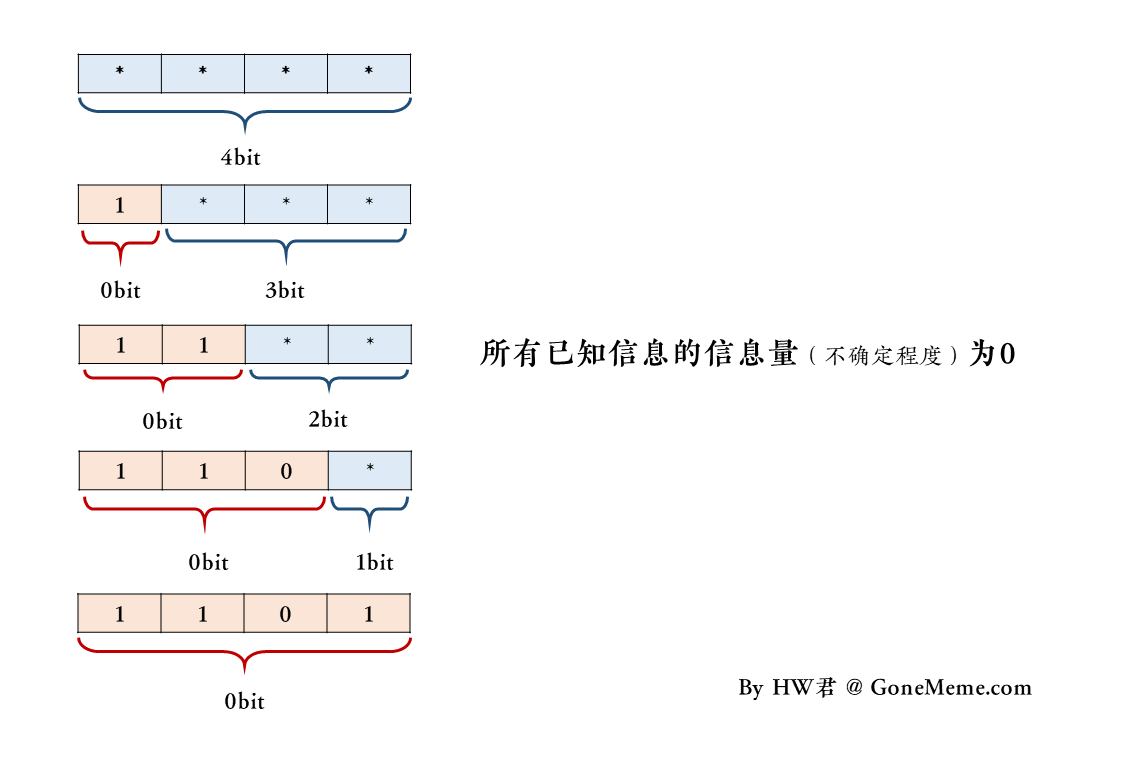
为了简化说明问题,我们假设有一个4bit的U盘。
我们用「*」来表示什么都没有记录,然后我们可以向U盘里拷贝「0」或「1」的文件。
在初始状态下,U盘的空闲容量和总容量均为4bit,初始状态可以表示为「****」。
然后HW君往U盘里复制了一个文件「1」,那么此时U盘的状态更新为「1***」。
此时U盘已用容量为1bit,空闲容量为3bit,复制的这个文件的大小为1bit,U盘的总容量为4bit。
然后HW君继续复制剩下的3个数据,最终U盘的状态更新为「1101」。
在这个过程中间,我们可以描述这样的一个瞬间:
当HW君把大小3bit的文件「110」复制进这个大小4bit的U盘「****」后,
HW君得到了一个总容量4bit的U盘,其中已用容量为3bit,空闲容量为1bit,状态为「110*」。
这样的一个司空见惯的表述,有没有问题呢?
有的,那个大小为3bit的文件「110」,用香农信息量公式算得的熵是0bit。
它是已知的,没有不确定性。
但是我们平时还是一直会认为那个「110」的文件,其熵就是3bit。
这其实也就是补丁1的说法。
这其实是一个符合直觉的混淆。
当我们说「110」这个文件的大小是3bit时,我们是说「110」这个文件占用了一个状态为「***」的空间,这个「***」空间的熵为3bit。
而状态为「110」的信息,用香农信息量公式求得的熵是0bit。
我们认为「110」的大小是3bit,是在说另一个虚拟的熵系统「***」的熵是3bit。
这里HW君将这类虚拟出来的熵系统称为「指代熵系统」。
信息「110」和指代熵系统「***」是两个完全不相同的事物。
「110」是一个0bit的0熵系统,而「***」是一个3bit的熵系统。
但是人们常常用后一个虚构的指代熵系统来指代一个确定的0熵系统。
这种指代在大多数情况下不会产生什么影响,直到我们开始进行一些涉及细枝末节的哲学思考。
这里我们把状态为「****」的4bit的U盘看做一个等待测量的「被测熵系统」。
那么「1」「11」「110」「1101」就是4种不同类型的「尺熵系统」。
这4个尺熵系统的熵为0,可以用来测量被测熵系统的熵,得到同一个被测熵系统「****」的不同的熵。
而人们也会用「*」「**」「***」「****」这四个指代熵系统,来分别指代「1」「11」「110」「1101」这四个熵为0的尺熵系统。
那么还有一个问题就是,如何知道「1」「11」「110」「1101」这4个尺熵系统的熵为0?
3. 通信的元尺熵系统
香农构建起来的现代通信体系中,往往一定会基于这么一个前提:
抛一枚硬币,要么是正面,要么是反面。
在数字电路中,要么是高电平,要么是低电平。
一个bit的状态,要么是0,要么是1。
…
这样的一种表述即构建起了一个通信过程中最底层的「元尺熵系统」。
这样的表述它本身可以构成一个熵系统,这个系统可以用来测量所有现代通信工程中的信息的熵。
基于这个元尺熵系统,可以测得「1」「11」「110」「1101」这些信息的熵都为0。
因此HW君在上一期认为信息都是0熵系统,现在看来还是有点武断了。
当我们用现代通信技术发送一个信息时,例如发送「110」。
我们可以把这个信息当作一个被测熵系统,然后用元尺熵系统测量这个信息,就可以得到信息的熵为0。
例如「110」这个信息,用元尺熵系统进行测量,它的熵是0。
但是日常生活中,我们会用另一个虚拟的熵系统「***」来指代「110」。
而这个指代熵系统「***」用元尺熵系统测量出来的熵是3bit。
当这个信息发送之后被接受者接收,接受者便不再将它视为一个用元尺熵系统测量的被测熵系统,而是作为一个尺熵系统来使用,以测量其他被测熵系统。
例如我们把「110」当作一个尺熵系统,用它去测量另一个熵系统「****」的熵。
那么被测熵系统「****」的熵是1bit。
但尺熵系统「110」的熵仍然为0。
而如果用同一个尺熵系统「110」去测量另一个被测熵系统「*****」。
那么被测熵系统「*****」的熵是2bit。
因此同一个信息「110」,作为被测熵系统而被元尺熵系统测量时,其熵为0。
而作为尺熵系统去测量不同的被测熵系统时,可以得到不同被测熵系统的不同熵值。
而同时,「110」还对应着一个虚拟的指代熵系统。
这个指代熵系统用元尺熵系统进行测量的结果是3bit。
而无论是「尺熵系统」、「被测熵系统」、「指代熵系统」还是「元尺熵系统」,对它们的熵值的求解都满足香农信息量公式。
4. 谁的信息量
我们在上一期《信息哲学 | #2 信息的HW诠释》结尾留下了这么一个问题:
为什么获知一个新的信息(0熵系统),会让人感觉获得了更多的信息量(熵)。
要回答这个问题,则需要先分辨出,当我们在谈论「信息量」时,我们到底在谈论些什么。
我们日常语境中,对于「信息量」的说法其实混成一锅粥。
当我们在说某一个信息的信息量时,究竟是在说哪种类型的信息量:
(1)这个信息作为被测熵系统,基于元尺熵系统的熵。
(2)这个信息作为被测熵系统,基于某个尺熵系统的熵。
(3)这个信息作为尺熵系统,某个被测熵系统基于这个信息的熵。
(4)这个信息的某个指代熵系统,基于元尺熵系统的熵。
(5)这个信息的某个指代熵系统,基于某个尺熵系统的熵。
(6)这个信息的某个指代熵系统作为尺熵系统,某个被测熵系统基于这个指代熵系统的熵。
…
这些情况非常多,令人头疼。
不过我们有2个灯塔可以避免迷路:
(A)熵的测量至少涉及到2个系统
(B)熵的结果都满足香农信息量公式。
绝大多数对于熵/信息量的争论,其实是在基本概念上的混淆。
争论的双方说的并不是同一个类型的信息量。
(本章节完,尽请期待下一节)
By HW君 @ 2021-05-06
或者我猜作者觉得负号的哲学意义很重要是因为试图捋清信息学的“熵”和物理学的“熵”的关系? 我上面评论主要着眼点在计算上,所以觉得负号不重要。这个问题的话,可能确有讨论的意义
先看个三元一次方程组的问题,做引子
Q1) 3个未知数xyz,1个方程
Q2) 3个未知数xyz,2个方程
Q3) 3个未知数xyz,3个方程
3个问题中约束条件数目(即方程数)1、2、3递增;3个问题的解空间维数2、1、0递减。试问:用约束条件定义信息还是用解空间维数定义信息?对于上面3个未知数方程组的例子:
#(约束条件) + #(解空间维数) = #(未知数)
或者再翻译下,
(约束限制的自由度) + (已知约束条件后的自由度) = (无约束的自由度)
上面方程组未知数个数是否等于3不那么重要,比如现在突然说还有第4个未知数w,无非把上面的:
1+2 = 2+1 = 3+0 = 3,
每一项加1,换成:
1+3 = 2+2 = 3+1 = 4,
描述的规律还是不变的。
类比到信息熵的问题,
对于信息M来说,
#(M的不确定性) + #(M已知后不确定性) = #(M未知时的不确定性)
其实是否给上式的每一项乘以“-1”不重要,想把上式的“#()”或者“-#()”叫做什么也不重要,这个A+B=C的数学关系是不被破坏的,实际应用中就是最朴素的平均编码长度来刻画的:
有状态S和用于描述该状态S的信息M,则:
MeanLength(M的编码) + MeanLength(M已知,描述状态S的编码)
= MeanLength(M未知,描述状态S的编码)
编码长度对应了可描述的范围大小,每一个bit的确定都让可描述范围坍缩了一定程度,如同引子问题里随着方程数量的递增,解空间终归坍缩到0维的唯一解(排除无解的特殊情况)。如果外星文明使用的是3进制,把式子里的log从底数2换成底数3,相当于乘了一个常系数而已,上式仍然成立。
维纳省略负号,无非乘了一个-1,形式上省事;香农带上负号,计算时都是正值,数值呈现起来省事。在我看来,有一套定义和记号,该定义下有一组数学关系恒成立,就够了。数学的研究对象不是“数”,而是关系
两个数学细节,尤其第二个,作者可能理解有误,啰嗦几句:
(下面均使用香农的有负号版本的信息熵讨论问题)
1)从硬币、骰子的离散分布的信息熵(概率的求和式),不能自然推广到连续分布的信息熵(概率密度的积分式),二者并不等价,差额的那部分可以藉由连续分布的无限加细发散到无穷。所以信息熵的积分形式,哪怕该积分式可积,也不能类比于硬币的log(2),骰子的log(6)。如果严格按离散情况的定义,任何连续分布的信息熵都是无穷大
简单的例子:
不存在一个编码系统,可以用有限位编码表示有限区间[0,1]上的每个实数。不丧失精度意味着编码无限长。
其(离散情形定义下的)信息熵是发散到无穷的;但该分布的积分形式是可积的,可以动手算出log(1) = 0。
2)互信息的定义有误,互信息一般习惯记号为I,有:
I(X, Y) = H(X) + H(Y) – H(X, Y) = H(X) – H(X | Y) = H(Y) – H(Y | X) ,
互信息恒非负,而作者似乎把互信息误记为H(X, Y)
延伸到上一段的连续概率密度的积分形式,这里有一个有趣的事实:
H(X), H(Y), H(X, Y)这三个值可以发散到无穷,而I(X, Y)可以是有限值。
此类情形里,I(X, Y)反而比更基础的概念H()更有实际意义。用个不严格的表达:全体整数和全体奇数的二进制编码都是无穷长的,但奇数编码可以比整数编码“短”1。
挺喜欢作者的哲学科普视频和文章的,但这个问题上好像有点“坐而论道”了。个人来说,不觉得这个“负号”配得上这样长篇的“哲学式”的讨论。算一两道题,或者解决点实际问题,就知道哪些是本质的、精华的规律,哪些只是枝枝蔓蔓。
令我欣慰的是,终于有人评论这篇文章了。
令我沮丧的是,目前的我并不能很好地理解你的评论中涉及的专业知识。
也许有一天我系统完整地学习过信息论之后,才有资格回复你的这条评论。
因此现在我只能回复你,这个负号在应用上可能没有影响,但是对于哲学意义上的诠释来说却很重要(至少我直觉上觉得它很重要,但也有可能我错得离谱吧)。
我举个例子吧,信息熵的式子里有log,log有底数这个参数,人类常用的有自然对数ln(底数e,数学上至简)、2为底的对数(计算机2进制)、10为底的对数(人类历史沿革的10进制、数量级),这些都是log,信息熵用哪个log呢?结论是都可以,用任何一个都不影响使用,这也是我举例说的,如果外星人三进制,ta们的信息论仍然和我们的结论一致。这个信息时代,充满了二进制,log2自然更常用一点,底数为2再带上负号的香农版本定义,可以直接对应到二进制编码的平均长度,更有“实在”意义。
说到底,中学数学里的对数的换底公式log_a(x) = ln(x)/ln(a)就够理解这些话了,对于底数a的log_a,应用时参与计算的每一项都多乘一个1/ln(a)的常系数罢了,这个常数当然可以穿透信息熵定义里的求和号、积分号,来到方程的最外层。就像解方程时,等号两边乘以一个不为0的数,可以认为方程还是原来的方程,乘以-1当然也可以。我还是倾向于认为香农和维纳只是各自习惯的选择罢了。当然我也没系统学习过信息论,只是浅浅用过一点儿相关知识,仅供参考。