文 | HW君
A Philosophical Theory of Information
0. 一个被忽视的负号
这是一个新的系列「信息哲学」。
距离《逻辑 | 我向你发送了一条负信息》一文发布已经过去将近半年,在那篇文章里HW君留下了许多悬而未决的疑问。
这半年来HW君久久无法释怀,一直在对「信息」和「熵」的概念进行重新思考。
对这些底层基础概念的重新理解,重塑了HW君的整个观念体系,也导致了以前的许多文章都需要重写。
总的来说,HW君并没有「完全想明白」,但也是时候开始着手去做点什么了。
在还没准备好的情况下写作「信息哲学」这个系列,算是为自己梳理长久以来的思路。
在这个过程中,一些原有的观念发生改变,一些原本混乱的模糊得到解答,但更多的时候仍然是直面自己的无知。
1948年,香农(Claude Shannon)的《通信的数学原理》(A Mathematical Theory of Communication)横空出世,开启了今日波澜壮阔的信息时代。
随之而来的,还有对于「信息」这一概念的巨大混淆。
互联网上存在着这样的两种争论:
(1)信息是熵。
(2)信息是负熵。
香农本人的观点是「信息是熵」。
而最早提出「信息是负熵」的应该是维纳(Norbert Wiener)。
维纳是另一位和香农几乎在同一时期对「信息」进行理论构建的大师。
维纳曾在麻省理工学院教过香农,给了香农许多启发。
维纳在其集大成著作《控制论》一书中,通过分析直流电路来研究「信息」,从而推导出信息论的部分理论基础。
维纳和香农的信息量公式,从形式上看只差了一个负号。
基于这个负号的差别,香农认为「信息是熵」,而维纳认为「信息是负熵」。
由此开启了信息论历史上最大的混淆。
许多人选择忽视这个负号,包括香农自己也觉得这只是「数学上的文字游戏」(mathematical pun),认为其无关紧要。
但这其中细微之处造成的混乱一直延续到了今天。
于是就出现了诡异的一幕。
在香农信息论领域里,学术界持有类似香农的观点:
信息具有不确定性。
不确定程度越大,信息量越大。
信息是熵。
但在将信息与日常生活关联、进行诠释的时候,人们又不约而同转向维纳的看法:
信息具有确定性,可以消除不确定性。
不确定程度越小,信息量越大。
信息是负熵。
这是两种截然相反的表述,竟可以共存于同一个清醒的头脑之中。
今天有无数的人学习过或正在学习信息论,但却很少有人会觉得这里面有所不妥。
这完全是两种矛盾对立的观点,人们若无其事选择忽略这种冲突,以至于产生了如此严重的「灯下黑」。
历史上,香农在其书信和报告中,说法都是「信息是熵」。
第一个提出「信息是负熵」观点的是维纳,而这个观点也被更广泛接受,因为它更符合直觉。
但如果我们翻看维纳《控制论》中对于「信息量」公式的推导,就会发现公式一开始是有负号的,只是维纳为了让公式符合直觉中途丢掉了负号而已。
本文末尾的附录里,HW君会说明维纳是如何丢掉这个负号的。
这个负号并不会影响工程师们对香农信息量公式的应用,其带来的理解上的细微差异并不会妨碍人们构建起今日波澜壮阔的信息时代。
但对这个负号的认识会影响到我们对这个世界的看法,影响到我们对于信息的哲学诠释。
而我们这个「信息哲学」系列文章,就是从这个被忽视的负号开始。
这个系列的文章会分为几期,围绕着「信息」与「熵」的话题进行展开。
本文我们先会复盘这个混淆是怎么产生的。
下一期文章则尝试给出一个解释这种混淆的诠释。
1. 香农的两个思维翻转
1940年代,正值第二次世界大战之际,在贝尔实验室帮助美军破解密码的日子里,香农面对的问题是如何从一些杂乱无章的符文密码中解读出正确文本。
当时贝尔实验室的密码工程师们普遍都需要操心声音、电流、波形等具体事物,但香农把「信息」从具体的物理世界剥离出来,为它建立了一套纯数学的理论。
香农构建出一整套代数方法、定理和证明,使得可以对「信息」进行更谨慎的研究。
这套方法需要人们对以往的思维模式进行彻底的翻转。
于是香农抛出的第一个「思维翻转」便是:
信息就是信息,而不是物质或者能量。
当然上述这句话其实是维纳说的,维纳给了香农很多启发。
那些战争中各式各样的加密通信活动,无论是信件、声音、广播、电报、电话……其通信的形式可以多种多样,但内核都是相同的。
所以要对「信息」进行更深入理解,发现其隐藏的模式,就需要扫除这些包裹在「信息」外层的不同形式。
假设HW君发送了一串只有0和1的二进制数字给你,它是「1101」。
那么这串二进制数字「1101」可以被称为「信息」。
同样的「0」和「101101」也都可以被称为信息。
不局限于二进制,十进制的「2021」也可以被称为信息。
并且不局限于数字,一串字母「GoneMmeme」也可以被称为信息。
当然,单个字母「H」或者「W」也可以称为信息。
更进一步,一个或一串汉字「消失的模因」也可以被称为信息。
一幅图像或者一段声音也可以被称为信息。
……
这样的对于信息的理解符合我们的直观感受。
「信息」是一些可以传递某些意义的符号或者标记,它可以拥有不同的物理形式。
如果我们抛开蕴含在「信息」中的意义不谈,那么信息就只是某些特定的物质。
例如纸张上特定路径的墨水、屏幕发出特定颜色组合的光、具有某个特征的声波、计算机电路状态的通和断……
而维持这些特定形式的物质,常常需要消耗能量。
所以即便我们认为「信息不是物质和能量」,也仍然可以断言:
信息的存在依赖物质和能量。
但我们关注的并不是物质和能量,而是信息,以及信息背后所能传递的意义。
后来香农证明了,世界上的所有信息的确都遵循着同一套数学规则,无论它们的物理形式是什么样的。
这种「思维翻转」让今日互联网的存在有了理论基础。
于是无论是声音、图像、文字……它们都可以依靠香农的数学规则转变并储存为一份二进制文件,透过电信号在网络中传播。
而随后香农还抛出了第二个更加违反直觉感受的「思维翻转」:
通信和「意义」无关,而和「不确定性」有关。
在当时协助美军的大多数密码工程师看来,通信的基本问题是使自己的意图被接收的人理解,从而传递「意义」。
但在香农看来,通信的基本问题是「如何在一点精确地复现出另一点的消息」。
这个问题和「意义」无关,而和「不确定性」有关。
这样的思维翻转重新界定了通信工程的工作范围。
即一个通信工程师根本不需要关心A想向B发送的消息有什么意义,他只需要将A的消息精确地复现给B,而不必理解其意义。
香农的这个思维翻转与香农的工作经历有关。
在协助美军破解密码的日子里,香农经常要面对一串看上去毫无意义的数据流,然后从中找出真正的信号。
在这个过程中,香农发现其实并不太需要去关心这些密码真正的意义是什么,他要做的只是统计每个字符出现的概率并进行猜测。
一份看上去像是随机乱码的字符数据流,我们可以通过大量地统计发现它隐藏的普遍模式:
(1)英语中e和t出现的频率比较大,而z和j的频率比较小。
(2)最常出现的双字母组合是th,大概每一千个单词出现168次,紧随其后的是he、an、re和er,还有一些双字母组合的出现频率为零。
(3)紧跟在q后面的字母u是冗余,去掉后没有影响。
(4)在单词an后面,以辅音字母开头的单词出现的概率极小。
(5)假如一个字母以u结尾,那么这个单词是you的概率极大。
(6)连续出现两个相同字符时,它们通常会是ll、ee、ss或oo。
……
应用这种纯粹数学统计的结果便是,香农可以在完全不理会一份密码想传达的意义是什么的情况下,靠统计学猜出密码的真正内容。
这个思维翻转使得香农从头开始思考「信息」具有什么样的性质。
而香农最后给出的回答是:
信息具有不确定性。
不确定程度越大,信息量越大。
信息是熵。
2. 信息与不确定性
香农是如何得出这个结论的呢?
我们看这样的一个最简单的事件X:
(X)抛一枚均匀正反面的硬币。
其结果只有两种,要么「正面朝上」,我们记为1;要么「背面朝上」,我们记为2。
所以这个抛硬币的事件X有2种不确定的可能性结果,各自的概率都是1/2:
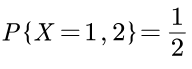
再看这样一个稍微复杂一点的事件Y:
(Y)抛一颗均匀六面的骰子。
其结果有六种,骰子点数可以是从1到6,我们同样将结果顺序标记为1到6。
即这个抛骰子的事件Y有六种不确定的可能性结果,从1到6,各自的概率是1/6:
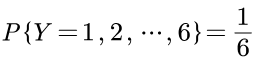
现在我们比较事件X和事件Y的不确定性,哪个事件的「不确定程度」更大一点?
直观感受显然是事件Y的不确定程度更大,因为它有6种可能。
那么可不可以对这种「不确定程度」用数学公式进行量化?
当然是可以的。
香农通过一系列严谨的推导,最后给出了的量化这种不确定性的香农信息公式:
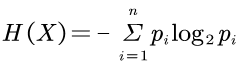
这个H就是当今香农信息论学术意义上的熵/ 信息熵/ 香农熵/ 信息量,单位是比特bit。
本文末尾的附录里,HW君会对这个公式进行详细分析。
这里我们简单地将上面抛硬币的事件X和抛骰子的事件Y代入信息公式里。
得到抛硬币的事件X的信息量是1bit:
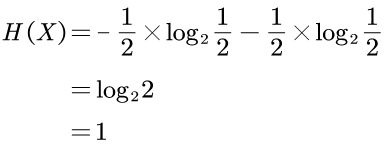
抛骰子的事件Y的信息量是log26,约为2.6bit:
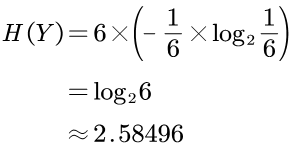
即可以得到 H(Y)>H(X)。
于是结论是,事件Y的信息量比事件X的大,也就是事件Y比事件X拥有更多的不确定性。
即抛骰子事件Y的熵比抛硬币事件X的熵大。
而这个计算结果的出发点是:
信息具有不确定性。
不确定程度越大,信息量越大。
信息是熵。
上述这3个命题便是香农对于香农信息公式的诠释结果。
这样的诠释是非常违反直觉的。
现实中对种观点也存在着非常多的争论。
例如维纳就认为「信息是负熵」,其诠释为:
信息具有确定性,可以消除不确定性。
不确定程度越小,信息量越大。
信息是负熵。
维纳的这种诠释是非常符合直觉的。
而薛定谔在1944年出版的著作《生命是什么》(香农到1948年才发表《通信的数学原理》)中也表述过「生命以负熵为生」。
虽然后来薛定谔在修订版本中将此表述更换为「生命以自由能为生」。
所以如果让薛定谔来描述信息的性质,HW君猜测薛定谔应该会赞同维纳的观点。
对于「信息是熵」和「信息是负熵」的说法谁对谁错、存在着什么问题,我们这里暂时先搁置争论,放在这个系列的下期文章中详细解答。
本文我们先复盘一下为什么人们会在这个问题上产生完全相反的分歧,以便更好地理解整个事情的脉络。
3. 违反日常感受的信息量
许多人并没有意识到香农于「信息」的理解和诠释跟我们日常生活中的感受截然不同。
我们使用上面的抛硬币事件作为例子,并给它增加一个更加具体的生活化场景。
假设A君抛出一枚均匀正反面的硬币,抛完后A君能看到结果。
而B君背对着A君,即B君看不到抛硬币的结果。
然后,A和B各自表述自己目前的情况:
A:抛硬币的结果是「正面向上」。
B:我不知道抛硬币的结果。
那么问题来了,A和B两个人谁说的话「信息量」大。
根据香农的信息量公式,A说了一个确定的事件,事件发生的概率是1,其「不确定程度」为0,所以信息量为0bit:
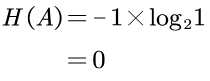
而B说了一个不确定的事情,正面和反面的概率都为1/2,其「不确定程度」为1,即信息量为1bit:
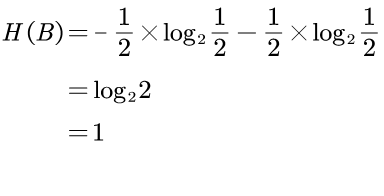
所以 H(B)>H(A),即B说的话「信息量」比较大。
更加准确来说,A说的话「信息量」为0,即完全没有信息量。
而这与我们日常生活的直观感受完全违背。
明明A说了更多的内容,B什么都没有说,怎么计算的结果是B的信息量比A大。
如果这还不够直观,我们可以假设连续抛硬币10次,同样A清楚全部的结果,而B完全不清楚。
那么产生如下的表述:
A:抛硬币的结果是「正反反正正正反正反反」。
B:我不知道抛硬币的结果。
在这种情况下,我们计算得到A表述的信息量为0,B表述的信息量为10bit。
于是当B不知道的事情更多时,计算出来的信息量还更大了。
在日常生活中,我们经常说某个人说话言简意赅,字字珠玑命中要害,会被形容为「信息量很大」。
而另外一个人口若悬河,但是废话连篇,没有营养,说了很多但给人感觉什么都没有说,即「信息量很小」。
但在香农信息论的世界里,情况却是反过来的。
在上面抛硬币的事件里,A完整地描述了硬币抛得的情况,但其信息量却是0;
而B什么都说不出来,但其信息量却要比A远大得多。
并且B越不确定,信息量反而越大。
信息量公式的这种对现实生活直观感受的违背也影响到了维纳。
维纳在推导信息量公式时,按照日常生活直觉认为「信息具有确定性,能够消除不确定性」,所以他在信息量公式的推导过程中丢弃了负号,并提出「负熵」的概念,试图让公式更加符合直觉。
这样的结果就是,出现了两种对于信息的诠释,它们之间是互相矛盾的。
而产生这种矛盾的原因可能有下列3种情况:
(1)香农信息公式是错误的。
情况(1)的概率是最小的,因为香农信息公式已经被反复证明是成立的。
人们对香农信息量公式的应用取得了令人瞩目的成就,难道这些成就都是建立在错误的地基上的?
今日这个波澜壮阔的信息时代正是香农信息量公式正确性的最好辩护。
(2)维纳的诠释是错误的,即人们的直觉是错误的。
情况(2)说明了我们的直觉是不靠谱的,此类情况在历史上已经发生多次。
例如地球不是平的而是一个球,太阳不绕地球转而是地球绕太阳转。
如果是这种情况,那么我们应该调整自己的认知去适应公式,而不是让修改公式适应我们的直觉。
(3)香农的诠释是错误的,不符合人们直觉。
情况(3)HW君:香农只是个数学家,他根本就不懂香农信息论。
4. 调和矛盾的补丁
并不是说只有HW君发现了这个问题。
相反,有非常多的人意识到了这种矛盾感。
为了方便讨论,这里我们把日常生活中符合直觉的那个信息量概念称为「日常信息量」,而把香农诠释的那个信息量称为「香农信息量」。
我们以抛一次硬币的事件X作为例子。
抛一次枚均匀硬币,A知道结果,B不知道结果,那么:
A:抛硬币的结果是「正面向上」。
B:我不知道抛硬币的结果。
那么B的香农信息量为1bit,A的香农信息量为0bit。
即可以表述为:
B的香农信息量比A的香农信息量大。
我们称这个结论符合「信息的香农诠释」。
但我们日常生活的直觉是,A的话信息量要比B的大,B的话一点信息量都没有。
即可以表述为:
A的日常信息量比B的日常信息量大。
我们称这个结论符合「信息的日常诠释」。
也就说说,公式算得的「香农信息量」和根据直觉感受到的「日常信息量」是矛盾的,对应着两种截然相反的诠释。
在意识到矛盾之后,许多人试图给出一些相应的补丁,以弥合这种矛盾。
4.1 补丁1:已知与未知
最常见的补丁便是引入时间概念,把信息分成「已知信息」的和「未知信息」两部分:
- 补丁1:已知与未知
日常信息量:已知信息的信息量。
香农信息量:未知信息的信息量。
将这个「补丁1」代入事件X中,我们就可以对这种矛盾进行重新调和:
A:
A的香农信息量很小,因为A没有未知信息。
A的日常信息量很大,因为A有很多已知信息。
B:
B的香农信息量很大,因为B有很多未知信息。
B的日常信息量很小,因为B没有已知信息。
在打上了这个「补丁1」之后,一切就又好像「合理」了起来。
而类似诠释方法,还有:
- 补丁1.1:输入信息消除不确定性
香农信息量:越不确定,需要输入的信息量越大。
日常信息量:越不确定,已经输入的信息量越小。
以及
- 补丁1.2:正说和反说
香农信息量:还能再说什么
日常信息量:已经说了什么
不过在HW君看来,「补丁1.1」和「补丁1.2」都是同一类,是「补丁1」的马甲。
它们都把信息分成了「已知信息」和「未知信息」的两个部分。
实话实说,像「补丁1」这样用时间来解释矛盾的说法非常具有迷惑性,不仔细分析的话很难发现其中的问题。
假设这样一个场景,A君连续抛硬币4次。
这里用0表示正面,用1表示反面,*表示未知,现在抛4次硬币的结果为「1101」。
那么按照「补丁1」的逻辑有:
在最初,A不知道抛硬币的结果,那么A已知信息的信息量为0bit,未知信息的信息量为4bit,记为「****」。
当A看到了第一枚硬币的结果之后,那么A的已知信息的信息量变为1bit,未知信息的信息量就变为3bit,记为「1***」。
当A看到了第二枚硬币的结果之后,那么A的已知信息的信息量变为2bit,未知信息的信息量就变为2bit,记为「11**」。
当A看到了第三枚硬币的结果之后,那么A的已知信息的信息量变为3bit,未知信息的信息量就变为1bit,记为「110*」。
当A看到了第四枚硬币的结果之后,那么A的已知信息的信息量变为4bit,未知信息的信息量就变为0bit,记为「1101」。
这样的逻辑看上去是不是非常「合理」。
然而它只是看上去合理。
真相是什么?
「补丁1」的问题出在哪里?
答案是,不存在这样的一个信息量会发生变化的「已知信息」。
或者说,上面的所有已知信息的信息量都应该是0bit。
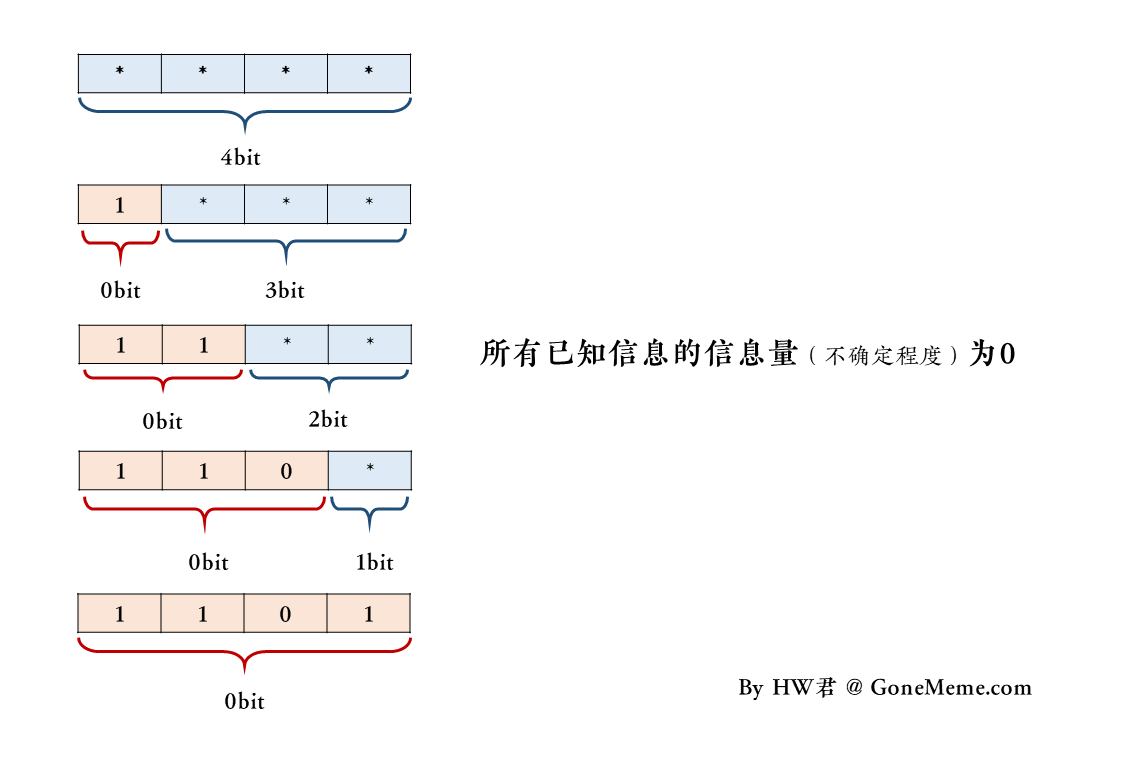
所谓「已知信息」的信息量,也就是「已知信息」的「不确定程度」。
但既然是已知的,那就是确定的,其不确定程度一定为0。
即按照「补丁1」的逻辑,其「日常信息量」都应该一直恒为0bit,它不会有一个变大或者变小的过程。
同样的,「补丁1.1」的「已输入消息」和「补丁1.2」的「已经说了什么」的部分的信息量,都恒为0bit。
到这里我们可以得到一个确定的结论:
所有已知的信息,没有不确定性。
「已知的」就是「确定的」,所有确定的信息,没有不确定性。
它是一个同义反复,是个真命题。
因此类似「补丁1」的说法,在逻辑是不自洽的。
这个不自洽非常难被发现。
4.2 补丁2:不同的概念
其实相当多的人意识到了「补丁1」的问题, 发现香农信息论中的香农信息量与我们生活里使用的日常信息量概念的矛盾无法调和。
这种情况下他们不再试图弥合这种矛盾,而是否认两种信息概念本身是相同的。
这种思路即可以表述为:
补丁2:香农信息≠日常信息
「补丁2」和「补丁1」的差异为:
「补丁1」认为,「香农信息量」和「日常信息量」之所以会不同,原因是「香农」(未知)和「日常」(已知)是不同的,而「信息量」是相同的,两个概念共享一个数学性质相同的「信息」。
即同一个物体,它可以被分为「香农部分」和「日常部分」这两个不同部分,对这两个不同部分用同一个数学公式求得的「信息量」结果不同。
「补丁2」认为,「香农信息量」和「日常信息量」之所以会不同,原因是「香农信息」和「日常信息」是不同的,因此它们的「量」的计算方式也是不同的,也就是存在两种数学性质不同的「量」,尽管它们都被称为「信息量」。
即同一个物体,它作为一个整体不可以被分割,但存在两个不同的数学公式一个是「香农公式」另一个是「日常公式」,用这两个不同的数学公式可以对同一个物体求得两个不同的结果,这两个不同的结果看上去恰好是相反的,因此会和我们的直觉相违背。
「补丁2」的逻辑便是,既然这两种信息量的大小总是无法一致,那就说明了同一信息中存在着两种完全不同的「信息量」。
即香农信息论中的「香农信息量」和我们生活中使用的「日常信息量」是完全不同的两个东西,虽然都被叫做「信息量」。
在研究通信原理和进行工程实践时,人们选择使用「香农信息量」的概念去进行计算和推演,它是管用的。
而回到日常生活中时,他们便重新使用回那个约定俗成的「日常信息量」的概念,它符合直觉。
大部分学习信息论的人都持有这样的观点,将学术和日常分隔开。
他们认为香农信息论中的「香农信息量」和我们日常生活中使用的那个「日常信息量」是完全不同的,企图将它们调和在一起是白费力气、无用的。
不过也有一部分人认真地思考过这个问题,但受限于各种原因没有得出有效的结论,于是最后选择妥协采取了「补丁2」。
HW君所尊敬的哲学家丹尼尔·丹尼特(Daniel C. Dennett)在其2017年的著作《From Bacteria to Bach and Back:The Evolution of Minds》第六章谈到信息时,就认为「香农信息」和我们日常生活中使用的信息概念不同,丹尼特称我们日常生活中使用的信息为「语义信息」(semantic information)。
他认为一条信息既有其「香农信息」也有其「语义信息」,并认为我们目前对于「语义信息」概念的了解所知甚少。
连丹尼特都无法对「信息」进行合理诠释,可见这个思维翻转的难度之大。
4.3 更优的补丁3
而从结果上看,「补丁2」的思路是优于「补丁1」的。
因为「补丁1」在逻辑上是不自洽的,而「补丁2」在逻辑上是自洽的。
但「补丁2」要求存在着两个独立的数学体系,一个用来解释「香农信息量」,另一个用来解释「日常信息量」。
两者并不兼容,也无法统一,但是又似乎刚好呈现出一种负相关的关系。
虽然「补丁2」遵循实用主义原则认为这两种信息是不同的,但它没有办法解释这两种信息为什么是不同的。
那么存不存在着一个更优的「补丁3」:
这个「补丁3」即是逻辑自洽的,避免犯类似「补丁1」的错误。
又可以用同一个数学体系来统一描述「香农信息量」和「日常信息量」,并诠释为什么公式的计算结果和我们的直观感受相反。
这样的一个「补丁3」显然会比「补丁2」要更加符合「奥卡姆剃刀原则」。
HW君的「信息哲学」系列文章,就是尝试给出这样的一个「补丁3」。
本文是此系列的第一篇,我们介绍了「信息论」的一个重大的混淆。
这个混淆给人们带来了非常违背日常生活直观感受的矛盾。
而针对这个矛盾,人们又发展出了一些补丁,试图调和这些矛盾。
但在HW君看来,这些补丁各有各的问题。
受限于篇幅,如何重新对「信息」进行哲学诠释,会放到下一期文章里详细展开。
下一期文章,HW君将会尝试回答这两个问题:
(1)「信息是熵」和「信息是负熵」的说法谁对谁错。
(2)为什么「公式算出的香农信息量」和「直观感受到的日常信息量」,两者大小是矛盾的。
5. 附录:香农与维纳的信息量推导
历史上,维纳和香农几乎在同一时期推导出了信息量公式。
维纳推导信息量公式是为了分析直流电路。
而香农推导的信息量公式在理论上会显得更纯粹和普适。
我们先看香农在1948年的《通信的数学原理》(A Mathematical Theory of Communication)论文的第6章(左)和附录2(右):

香农先假定了有一个事件集合,这些事件发生的概率为:
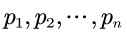
这些事件发生的概率是已知的,但究竟会发生什么,我们是不确定的。
然后我们用一个量H来度量这种不确定性,H是关于概率pi的函数,H反应了事件的不确定程度。
那么香农接着推论这个H需要满足这样的3个条件:
条件(1)H应当关于pi连续。
这里的「连续」是指对于所有的pi,都能找到一个与之对应的H,不会存在断点。
即在规定的体系内,所有的概率为pi的事件都必然会带来不确定程度H的改变。
即便是完全确定的概率pi=1,也会给系统增加大小为0的不确定程度。
不存在「在pi处没有H」的情况。
条件(2)如果所有pi都相等,即pi=1/n,则H应当是n的单调增函数。如果事件的可能性相等,那可能事件越多,选择或者说不确定性也更多。
这里讲的是等概率事件的信息量变化。
这和我们在文章第2小节的抛硬币事件X和抛骰子事件Y的例子类似。
一枚均匀正反面的硬币,抛得正面的概率和反面的相等,为1/2。
一颗均匀六面的骰子,抛得各个面的概率相等,为1/6。
因为抛骰子的可能事件越多,所以不确定程度越高。
因此H应当是n的单调增函数。
条件(3)如果一项选择被分解为两个连续选择,则原来的H应当是各个H值的加权和。
香农用了一张图来说明这个性质:
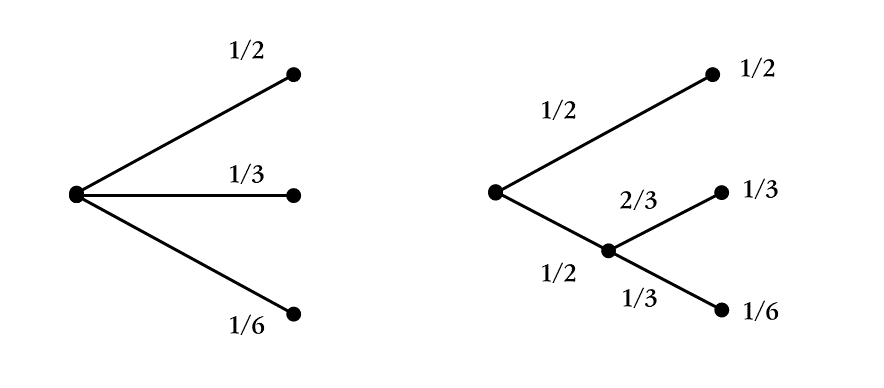
这里我们举一个更直观的例子。
假设有两个黑箱子,第一个黑箱子里有AB两个小球,第二个黑箱子里有xyz三个小球。
HW君在同一时刻伸手在两个箱子里各摸1个小球,那么摸到的结果组合起来可能会有6种情况:
Ax、Ay、Az、Bx、By、Bz
这6种情况发生的概率是相等的,都是1/6。
当然这里我们为它构造3个事件,以展示不同的概率。
事件1:摸到Ax或Ay或Az
事件2:摸到Bx或By
事件3:摸到Bz
那么很显然可以得到:
p1=1/2
p2=1/3
p3=1/6
现在HW君不再是同一时刻摸球了,而是将摸球的动作分解为两个连续的动作。
先从装AB小球的黑箱子的摸一个,再从装xyz小球的黑箱子里又摸一个。
我们单独看第一次动作,它会产生两种情况,可能摸到A或者B,概率为1/2。
事件a:摸到A
事件b:摸到B
事件的概率为:
pa=1/2
pb=1/2
而单独看第二次动作,它会产生三种情况,可能摸到x或y或z,概率各自为1/3。
我们同样构造一些事件:
事件m:摸到x或y
事件n:摸到z
则事件的概率为:
pm=2/3
pn=1/3
如果我们比较同时摸和分开摸的概率,就可以得到:
p1=pa=1/2
p2=pb*pn=1/3
p3=pb*pm=1/6
这里其实是在说明一个非常简单甚至都不需要明说的情况:
「同一时刻摸两个小球」和「分成两次连续摸,每次摸一个小球」这两个情况我们面对的概率是相同的,也即是这两种情况我们面对的不确定程度是相同的。
因此:
一个整体事件面对的不确定性H,会是各个子事件的H的加权和。
用H来表示上面的例子,即为:
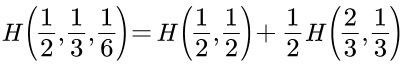
而满足条件(1)(2)(3)的H具有这样的形式:
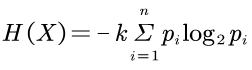
其中k是一个正的常数。
我们可以将k取1,即得到香农信息量公式:
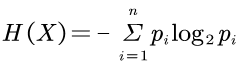
然后香农将这个量H称为「熵」。
香农还在附录2里进行更加详细地推论为何满足条件(1)(2)(3)的H一定是上面的这个形式。
这部分比较复杂,这里不详细展开,有兴趣的朋友可以自己查阅。
我们再来看一下维纳《控制论》中第三章对于信息量公式的推导:

维纳的信息量公式推导的难点在于二进制和十进制之间的切换,清楚这一点后比较好理解。
并且我们会很容易发现维纳在中途没有充分的理由便地丢掉了负号,并提出负熵的概念。
对于「如何测量信息量」,维纳从一个最简单的抛硬币事件开始构想。
抛一枚均匀正反面硬币,要么是正面,要么是反面。
我们可以用0表示正面,1表示反面。
那么可以认为最简单的抛一次硬币产生的信息量为1个单位。
构造一个无穷二进制小数,用来表示抛无限次硬币的过程:
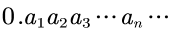
这里的每个an代表该二进制小数的第n位小数,数值是0或者1。
如果用十进制的a来表示这个无穷二进制小数,则可得:
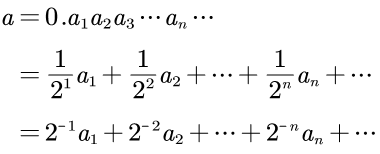
那么十进制数a的取值范围是0到1。
这些构造出来的数是为后面的场景服务。
然后维纳构建了一个使用这些数的场景。
假设数轴上有个从0到1的区间,表示事件的所有可能性。
然后有一个数随机均匀地落到这个0到1的区间上,表示随机事件的发生。
我们要怎么去测量这个数的值是多少?
最简单的测量方法就是二分法,也就是抛硬币:
首先确定这个数是否比1/2大,这是第一次判断;
然后再确定这个数是否比1/4或3/4大,这是第二次判断;
……
这样的二分法判断可以进行无限次,以不断逼近那个数值。
在这个过程中,我们每测量一次,就是做一次选择(抛一次硬币),产生1单位信息量。
那么上面构造的无穷二进制小数:
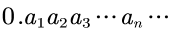
可以用来描述我们进行测量的全部过程。
而实际情况中,任何测量都是不完全精确的,我们假设这个测量过程中存在误差。
那么可以再构建另一个无穷二进制小数来描述这个误差:
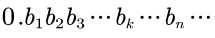
其中bn代表这个二进制小数的第n位数,其值是0或1。
而bk的值为1,在bk之前的所有值都为0。
同样,用十进制的b来表示这个二进制小数,则可得:
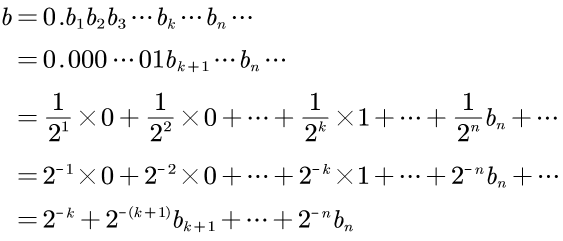
综合起来,随机均匀落在0到1区间的那个数我们用a表示,而测量的误差是b。
也就是实际测量时,测得的数为(a+b)。
因为从b1到bk-1都是0,所以a1到ak-1都是精确的,
而从第k位开始产生误差,后面的测量就都是没有意义的。
也就是,为了测量a值,我们进行了k次有意义的二分测量(抛了k次硬币)。
前面说了,每一次测量产生1单位信息量,那么k次测量产生k单位信息量。
那么求事件的信息量,就是要求这个k值。
如何求这个k值呢?
我们对误差b进行操作,可以得:
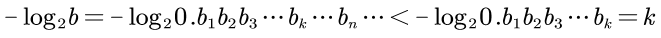
以及:
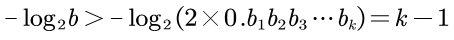
综上得到:
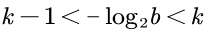
所以我们可以用-log2b来表示k值。
这里维纳的原话是:
The number of decisions made is certainly not far from
–log2.b1b2…bn…
and we shall take this quantity as the precise formula for the amount of information and its definition.
所做决定的数目当然接近于
–log2.b1b2…bn…
我们将取这个量作为信息量的精确公式和它的定义。
注意,此时维纳的信息量公式里是有负号的。
事实上,维纳推导出的这个信息量公式就是香农信息论中的自信息。
然后,维纳定义事件发生后增加的信息量为:
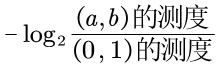
这里「(0,1)的测度」就是1,而「(a,b)的测度」就是b。
所以其结果仍然是-log2b。
到这一步,维纳的公式里还是有负号的。
后面接着的是将连续分布的概率乘上其信息量,再对其进行积分,思路其实和香农信息公式中的「加权和」相似,这里不作展开。
但是奇怪的事情发生了,到了公式(3.05)的时候,「log」前的负号被去掉了:
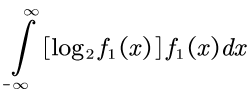
并且在去掉负号之后,维纳将这个信息量解释为熵的负数。
维纳当时的想法已经无从得知。
但HW君猜测,维纳觉得求得的这个量,它度量的是「不确定性」,这个量越大越不确定。
而我们在日常生活中的感受是:
信息具有确定性,可以消除不确定性。
不确定程度越小,信息量越大。
于是他将那个量取负值,以符合日常生活的直觉,然后提出「负熵」的概念。
维纳的原话是:
The quantity we here define as amount of information is the negative of the quantity usually defined as entropy in similar situations.
这里我们定义为信息量的量,是在类似情况下通常定义为熵的那个量的负数。
在HW君看来,维纳去掉负号的做法是考虑欠佳的。
面对同样的公式,香农选择相信公式,而维纳选择相信直觉。
但是香农对于公式的诠释,就是正确的吗?
(本章节完,尽请期待下一节)
By HW君 @ 2021-04-27
其实熵这个概念诞生之初,其意义也有分歧。
感谢up主更新