文 | HW君
0. 并不牢固的根基
说起来HW君在过去的文章里使用诸如「信息」、「熵」这些词已经相当长时间了。
不久前,因为想尝试写作新主题,HW君便重新开始梳理这些似乎早就习以为常的概念。
随后一下子陷入了深深的困惑之中。
夜里翻来覆去睡不着,忽然意识到HW君的许多文章都需要重写。
1. 信息论的建立
历史上,维纳和香农几乎在同一时期内对「信息」进行理论建立。
但香农的信息论更成体系,于是香农被视为是「信息论」的鼻祖。
维纳曾在麻省理工学院教过香农。
提起维纳,人们更多想到的是他鼎鼎大名的「控制论」。
维纳在其集大成著作《控制论》一书中,通过分析直流电路来研究「信息」,从而推导出信息论的部分理论基础。
维纳研究「信息」的目的是为了更好地研究他的「控制论」(Cybernetics)。
「控制论」同样也是个具有划时代意义的理论,我们今天常说的「赛博朋克」(Cyberpunk)就是「控制论」(Cybernetics)与「朋克」(Punk)的结合词。
在《控制论》一书中,维纳推导出的信息量公式的二进制表示是:
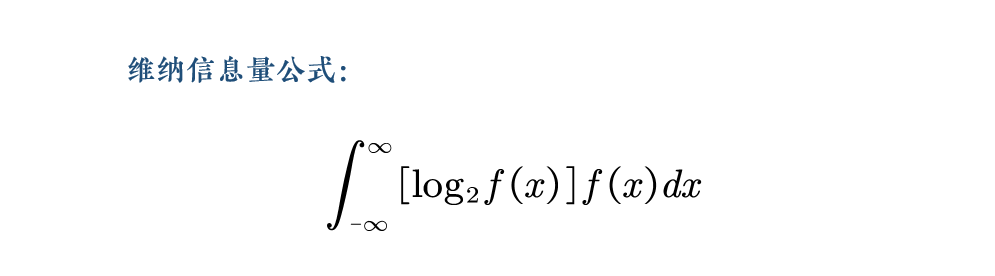
维纳推导出的信息量公式
而香农在构建信息论时,他正在贝尔实验室从事为美国军方破解敌军密码的工作。
在为军方破解密码的工作中,香农面对着各种杂乱无章的符文密码,他意识到自己需要建立一套彻底从物理细节中抽象出来的理论。
这套理论是脱离电流、声音、波形等物理性质的,它是纯数学的。
在1948年,香农发表了《通信的数学原理》(A Mathematical Theory of Communication),正式提出了「信息论」。
香农信息量公式的二进制表示是:
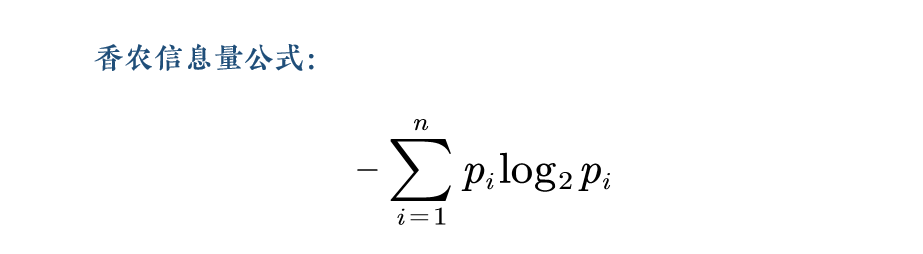
香农推导出的信息量公式
上面维纳和香农的这两个公式的目的基本是相同的,都是求一段信息的「信息量」。
但它们有两个比较主要的区别:
①. 维纳的表述是「连续」的,而香农是「离散」的。
②. 香农的公式比维纳多了一个负号。
造成①的原因之一有,维纳是从研究直流电路出发来推导通信之中的信息量。
因为电子元件中的电流是连续(模拟)的,所以维纳用微积分的思路来算信息量。
而香农那会儿在贝尔实验室面对的问题是如何帮美军破解敌方密码。
香农面对的是一个个杂乱无章的字符密码,所以他的思路是离散(数字)的。
这样造成的结果就是虽然公式的形式不太一样,不过两者的核心思路是一样的。
真正令人困惑的区别②中的那个负号。
那个负号反映了人们理解信息论过程中的各种困扰。
2. 信息的常见理解
在讨论那个负号之前,我们先快速看一眼香农的信息量公式。
现在信息论中的「熵」(entropy),也可以称为信息量、信息熵、香农熵。
1940年代,在贝尔实验室里破解密码的日子里,香农面对的问题是如何从一个个杂乱无章的符文密码中解读出正确文本。
香农需要构建出一整套代数方法、定理和证明,使得可以对「信息」进行严谨地研究。
首先第一步便是,如何对「信息」进行量化。
对某个东西进行量化,往往是科学研究的第一步。
我们经常用到各种度量单位,例如度量「质量」用「千克」,度量「时间」用「秒」。
下列是一些常见度量单位的国际定义:
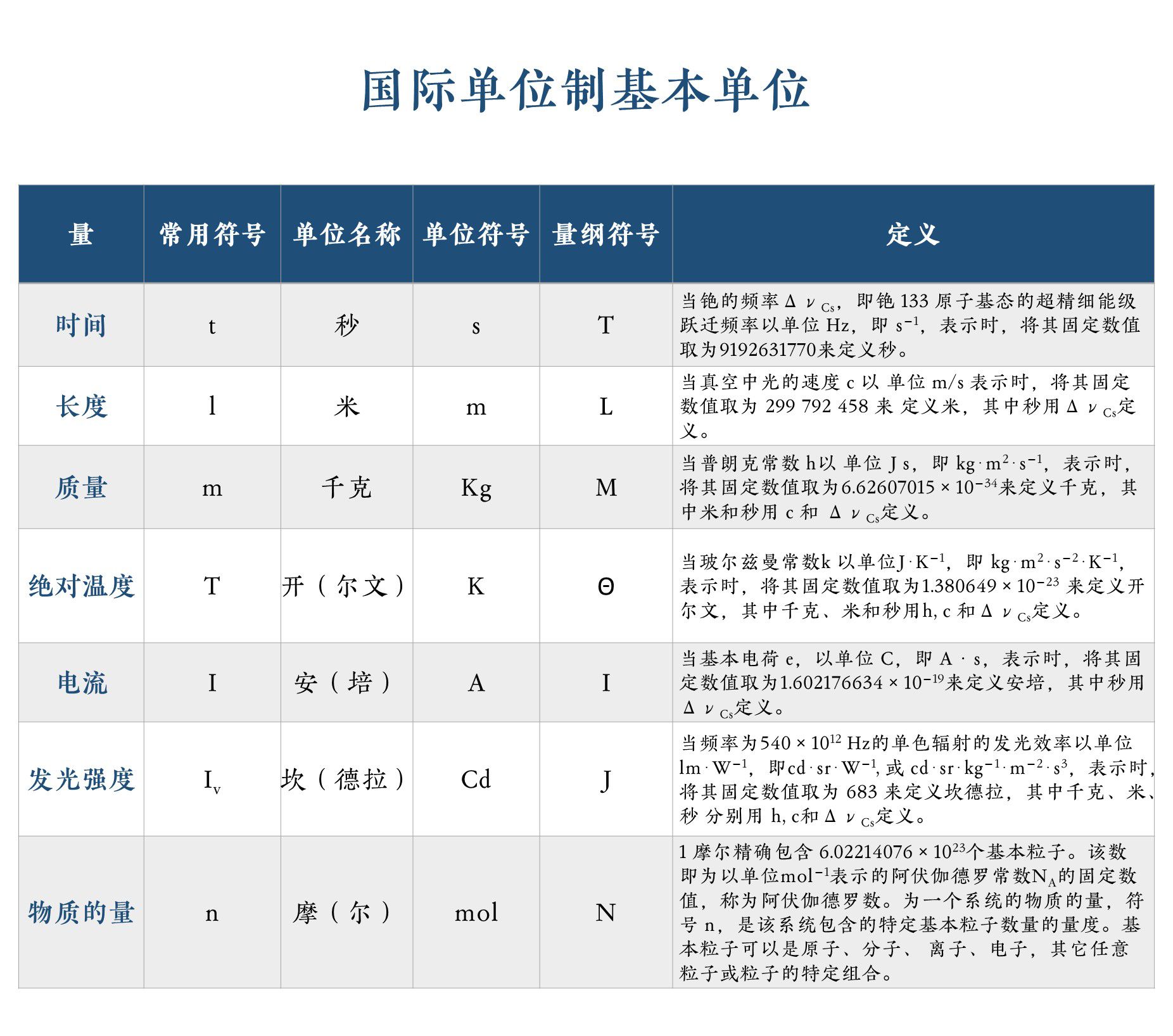
国际单位制基本单位
而我们今天知道了,二进制单位下,「信息」的最小单位是「bit」。
1bit反映在电子电路里就是元件电流的低电平或高电平,计算机读取为0或者1。
我们可以用最简单的「抛硬币」事件来描述「1bit」。
抛一枚均匀硬币,结果会有两种情况。
「正面向上」和「反面向上」的概率均为1/2 ,要么是正面向上,要么是反面向上。
这样的1次抛硬币事件所包含的信息量就是1bit 。
那么抛2次硬币包含的信息量就是2bit。
假设我们将「正面向上」表示为「0」,「反面向上」表示为「1」。
那么「抛2次硬币」的可能结果是「00」「01」「10」「11」一共4种。
也就是2bit信息量对应4种情况。
如果是3bit信息,也就是抛3次硬币,则会出现8种情况,分别是:
000、001、010、011、100、101、110、111
也就是说,抛n次硬币,会得到2n种可能的结果。
即n bit的信息对应着2n种情况。
反过来说,我们现在有1024种可能的抛硬币结果,需要抛硬币多少次?
或者说需要用多少bit的信息来存储这1024种情况?
n = log21024 = 10
答案是需要抛10次硬币,也就是包含10bit信息量。
在计算机上,1首普通MP3歌曲的容量大概是10MByte,换算成 bit 为:
10 MByte = 10*1024 KByte = 10*10242 Byte =10*10242 Byte * 8 = 83886080 bit
也就是为了让你能够听上一首歌,计算机抛了八千多万次硬币。
以上是对于「信息」的常见理解。
那么,它是准确的吗?
3. 信息的香农解释
作为一个民科,HW君长期以来也都是持有上文的那种理解。
但这样的理解是有问题的。
前段时间HW君翻了维纳《控制论》和香农《通信的数学原理》的原稿,发现上面那种理解其实是维纳的思路。
而香农的信息量公式虽然和维纳差不多,但他对于「信息」的理解和维纳是非常不同的。
1940年代在贝尔实验室里破解密码的日子里,香农面对的问题是如何从一个个杂乱无章的密码中解读出正确文本。
在这个过程中,香农是不关心文本的内容是什么的。
破解密码对他来说是一个纯粹的数学问题,香农要做的是去计算所有字母可能出现的概率。
再看上面说的「抛硬币」事件。
我们抛1次硬币,在未抛出硬币之前,它是一个不确定事件。
这个事件有两种不同的可能性,1/2概率正面向上,1/2概率反面向上。
对于香农来说,这个「抛1次硬币」事件存在着1bit共2种情况的不确定性。
现在我们连续抛3次硬币,即「抛3次硬币」为一个不确定事件。
那么「抛3次硬币」会有 23=8 种不确定的可能结果。
假如将正面向上记为0,反面向上记为1,则结果可能为:
000、001、010、011、100、101、110、111
这个事件存在着3bit共8种情况的不确定性。
好,现在我们抛出第1次硬币,结果是「正面向上」,记为「0」。
那么还剩下的2次抛硬币动作,则这个事件的可能结果更新为只剩下4种:
000、001、010、011、
100、101、110、111
此时,事件还存在着2bit共4种情况的不确定性。
我们继续抛第2次硬币,结果为1。
则这个事件的可能结果更新为只剩下2种:
000、001、010、011、100、101、110、111
此时,事件还存在着1bit共2种情况的不确定性。
接着抛第3次硬币,结果为0,事件的可能结果更新为只有1种。
000、001、010、011、100、101、110、111
此时,整个「抛3次硬币」事件的结果是「010」。
它已经是一个确定性事件,只有1种情况,存在着0bit的不确定性。
好了,现在我们可以把上面的「不确定性」换成「信息」或者「熵」。
这就是香农所理解的「信息」。
4. 一个负号
维纳和香农的信息量公式里,差了一个负号。
这个负号在大部分时间里不会影响计算结果,但是会影响我们对于「信息」的哲学诠释。
于是香农说,信息是熵。
而维纳说,信息是负熵。
这种正负之争,让HW君想起了另一个故事:
热力学的主要奠基人之一鲁道夫·克劳修斯在1865年首次引入了「熵」这个词。
克劳修斯意识到,蒸汽机的能量转换为功时,热量实际上并未损失,只是从较热的物体传递到了较冷的物体,并在传递途中做了功。
法国工程师卡诺把它比作一个水车,水从高处往低处流,水量并没有增加或者减少,但水在这个过程中做了功。
当所有的水都流到低处之后,它就无法再做功了。
克劳修斯想要度量的就是这种能量不可用、无法做功的程度,于是他用了「熵」(entropy)这个词。
有意思的是,著名的麦克斯韦在其《热理论》一书中建议,将「熵」的意思颠倒过来会更方便些,也就是定义为「能量的可用程度」:
这么一来,当系统的压力和温度变得均匀一致时,「熵」就耗尽了。
不过没过几年,麦克斯韦就转了一个180°发夹弯,决定沿用克劳修斯的用法。
他重写了《热理论》,并添加了一条略显尴尬的注脚:
在本书先前各版中,我曾认为,克劳修斯把他所引入的「熵」的概念定义为无法被转换为功的那部分能量,是不妥当的。
我进而将它重新定义为可用的能量,但这导致了热力学用语中的严重混乱。
因此,在这一版中,我已经努力遵循克劳修斯的原始定义来使用「熵」一词。
这里的问题不在于是像「还有半杯水」和「只剩半杯水」那样是「积极」地看待还是「消极」地看待能量的可用程度。
麦克斯韦先前把「熵」视为能量下属的一个类别「可做功的能量」,但其实「熵」是一个全新的度量。
HW君去翻了维纳《控制论》的那本书,维纳信息量公式的推导一开始是有负号的。
而那个负号是在中途被舍弃掉的,但维纳并没有说明原因。
HW君推测维纳是为了让结果更加符合人们日常生活里的直觉。
丢掉的这个负号并不会给信息理论的构建以及工程上的应用造成多大困扰。
但是却会影响哲学诠释!
在如今的信息论中,有着和这个负号类似情况的各种别扭说法。
例如,在信息论中我们赞同以下的论点:
系统的熵越大,不确定性就越大,包含的信息越多,信息量也越大。
注意以上命题在信息论中是正确的。
我们可以看上面提到的「抛3次硬币」的案例。
在我们抛第1次硬币之前,整个系统的熵最大,包含信息量最大,记为「???」,有3bit信息。
在我们抛完第3次硬币之后,整个系统的结果已经确定下来,记为「010」,它是一个确定事件,熵最小,有0bit信息,即信息量为0。
但上述过程和人们的直觉并不相符。
我们日常生活中的直觉是,在抛3次硬币之前,我们对结果一无所知,获得的信息是0bit 。
当我们把3次硬币都抛完之后,我们得到了3次确定的结果,那么我们获得3bit的信息。
但香农的信息量公式告诉我们,一开始拥有3bit信息,在抛完3次硬币之后,有0bit信息。
难道不是知道得越少,信息量越少;知道得越多,信息量就越多吗?
那么我们要相信直觉,还是相信公式?
维纳选择的是相信直觉,于是他把那个负号给去掉了。
而很多人虽然没有去掉负号,但是为了符合直觉,会把公式诠释得非常别扭。
例如很多人是这样解释那个负号的:
香农信息论中,「信息量不是说了多少,而是还能说多少」。
维纳信息论中,「信息量是消除一条消息的不确定性需要输入多少信息」。
此类怎么看怎么别扭的说法数不胜数。
类似的例子还有,例如「这本书信息量很大」这个命题。
这本书「信息量很大」,那么在信息论中这本书的「不确定性」很高,内容很混乱,可能几乎是乱码。
但我们日常生活里好像不是这么用的。
我们所说的「这本书信息量很大」指的是这本书能告诉我们很多信息,降低我们很多不确定性。
维纳和香农曾经讨论过这个负号,但他们的结论是这个负号是一个「文字游戏」。
这里我们可以对这个「文字游戏」做出澄清。
香农「信息论」中的「信息」是指 information。
而日常生活里「我给你发了一条信息」应改为「我给你发了一条消息」,「消息」是指 message。
所以香农说,信息是熵。
而维纳想说的是,消息是负熵。
他们指的不是同一个东西。
香农的思路是清晰的,「信息」就是不确定性,是熵。
维纳把公式里的「信息」和日常生活中使用的「消息」混淆在一起,于是舍弃公式里的负号以匹配这种混淆。
我们也可以保留「信息」的日常用法(message),然后把「香农信息论」中所涉及的「信息」替换为「熵」。
即「香农信息论」应更改为「香农熵论」。
相应的类似「信息量公式」应更改为「熵量公式」。
然后我们就可以仍然保留「信息」(message)的习惯用法。
但在这种情况下,我们对于「信息」(information)的哲学诠释仍然是有问题的。
5. 信息的哲学诠释
如果严格从香农信息论的公式出发,我们要如何对「信息」(information)作哲学诠释。
我们还是用上面那个「抛3次硬币」的例子来说明。
当我告诉你要「抛3次硬币」时,我告知了你一个体系,这个体系可能演化出8种不确定的结果:
000、001、010、011、100、101、110、111
此刻你增加了3bit的关于「抛3次硬币」体系的信息。
当抛完3次硬币得出「010」的消息之后,不确定性被消除,你有0bit的关于「抛3次硬币」体系的信息。
然后我们推广到日常生活,例如我发送了「GoneMeme」这一条文本消息给你。
当你接收到这条消息时,你得知了一个体系。
这个体系对不同人来说包含着不同的信息(不确定性、熵),也就是有着不同的信息量。
①. 对于一个不认识字的3岁小朋友来说,他看到的「GoneMeme」是一堆蓝白相间的色块,意义不明,有非常多的可能性,信息量非常大,小朋友甚至可以将这些字母理解成为几个排着队的小人。
②. 对于一个刚开始学英语的小学生来说,他认识「G/o/n/e/M/e/m/e」的每一个英文字母,但是他不懂这8个英文字母拼起来的单词是什么意思,所以对小学生来说,文本的信息量又缩小了一圈。
③. 而对于一个中学生来说,他认识单词「Gone」但不认识单词「Meme」,所以合在一起意思大概是「离开的Meme」,于是对于这个中学生来说,文本的不确定性又比小学生减少了,信息量又缩小了一圈。
④. 现在有一个大学生,他认识单词「Gone」,也读过几本关于「Meme」的书,当他看到「GoneMeme」时可能会翻译成「离开的迷因」,他会思考这个词可能有什么意思,并联想其他读过的关于「Meme」的书,对大学生来说文本的不确定性比中学生又少了许多,信息量又缩小了一圈。
⑤. 而对于本站的长期读者来说,当他们看到「GoneMeme」一词时,会知道它的准确中文翻译是「消失的模因」,他还知道它是个网站,运营者是HW君,以及HW君写了一些错漏百出的文章,那么对于「GoneMeme」的不确定性又缩小了很大一圈,信息量大大地减少了。
6. 我向你发送了一条负信息
我们把上面的过程拆开来看,就会发现「我向你发送一条消息」其实隐含了两个层次。
①. 我和你约定了一个体系,体系包含信息(不确定性)。
②. 我向你发送了一个消息,消息会减少体系的信息。
人们容易只盯着明显的②,而忽视了隐含的①。
那么抛开带来「信息」的「体系」,这个可以消除不确定性的「消息」究竟是什么东西呢?
HW君也并没有完全搞懂。
但既然「消息」可以减少体系的信息,那就姑且叫它「负信息」吧。
这就是这篇文章题目的由来。
但这种结论其实并不严谨,我们还需要更严格的代数证明。
这段时间HW君翻了一些统计物理学和认知科学的书籍,里面的数学公式都太过艰深晦涩,超出我的能力范围,完全看不懂。
所以此篇文章的推论也只能到此为止了。
这样的结论令HW君头疼不已。
深挖下去,HW君的许多文章在最基础的概念上就出现了致命问题。
而就算HW君及时发现,决定修正重写,也发现无从下手。
因为再往前,就到了统计物理学的领域了。
要想不陷入民科式的空想自嗨,就需要借助更高阶的数学理论工具。
而仅仅是窥其一角,就耗费了HW君如此大量的时间和精力。
哀吾生之须臾,羡长江之无穷。
(本章节完)
By HW君 @ 2020-09-23